Latin squares have various applications in Coding Theory, Cryptography, Finite Geometries and in the design of statistical experiments. Sudokus are a famous example of latin squares.
What is a Latin Square?
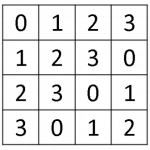
A latin square of order n is an n x n matrix containing n distinct symbols such that each symbol appears in each row and column exactly once. The symbols are usually denoted by 0, 1,…, n–1.
Example. latin square of order 4:
In the 1780s Leonhard Euler came up with the idea of latin squares while working on a problem which consisted of arraigning 36 officers of 6 ranks and from 6 regiments in a 6 by 6 square formation, such that each vertical line and each horizontal line of this formation is to contain one and only one officer of each rank and each regiment. Euler denoted the 6 regiments by the Latin letters and the 6 ranks by the Greek letters. He first arranged the Latin letters in a square so that no letter was missing or repeated in every row and column, he called this square a latin square; he did the same with the Greek letters and he called the superimposition of the squares a graeco-latin square.
In the 1930’s a big application area for latin squares was opened by Ronald A. Fisher who used them and other combinatorial structures in the design of statistical experiments. Fisher realized that latin squares could be abstracted from the partition of growing plots and applied to the elimination of systematic error in a much more general context. That is, for example, when growing plots with different fertilizers the systematic error due to variation in soil can be minimized by a suitable latin square partition of the plot:

A field planted with a crop using five different treatments according to a 5 x 5 latin square arrangement.
Orthogonality of Latin Squares
Given two latin squares of the same size we can superimpose them, that is, we can place or lay one latin square over the other to create a square of ordered pairs.
Example. When we superimpose two latin squares of order 4 we get a 4 x 4 square of ordered pairs:
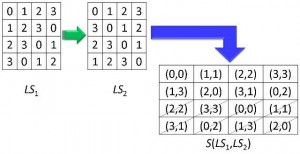
LSi and LSj are said to be r–orthogonal if you get r=N(LSi, LSj) distinct ordered pairs when you superimpose them. In the example above, LS1 and LS2 are said to be 8–orthogonal.
Moreover, two latin squares of order n are orthogonal if you get n2 distinct ordered pairs when you superimpose them.
Note that n ≤ r ≤ n2 for any pair of latin squares of order n.
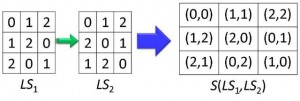
Example. Two latin squares LS1 and LS2 of order 3 are said to be orthogonal if we get N(LS1, LS2) = 32=9 distinct ordered pairs:
Orthogonality of more than two Latin Squares
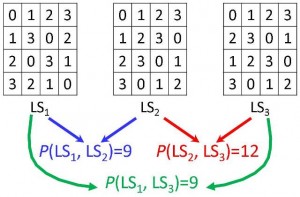
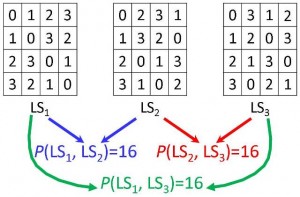
We can also generalize the concept of r–orthogonality to sets of more than two latin squares. In this case, given a set of t latin squares of order n, we superimpose all possible pairs of distinct latin squares and the sum of all the r–orthogonalities (i.e., the number of distinct ordered pairs that we get in each superimposition). This is called the rn(t)–orthogonality.
Example. Here we have a set of three latin squares of order 4 with r4(3) = 9 + 12 + 9 = 30:
A collection of two or more latin squares of order n is said to be mutually orthogonal (MOLS) if every pair of distinct latin squares in the collection is orthogonal.
Example. Let {LS1, LS2, LS3} be a set of 3 latin squares of order n. This set is orthogonal if OP(LS1, LS2)=n2, OP(LS2, LS3)=n2 and OP(LS1,LS3)=n2.
Example. Here we have a set of orthogonal latin squares of order 4:
Note that B(t, 2)n ≤ rn(t) ≤ B(t, 2)n2 for any set of t latin squares of order n and t ≤ n-1, where B(x,y) is the binomial coefficient of x and y.
The concept of MOLS of a given order is important, because it is known that there exists a projective plane with n points if and only if there are n–1 MOLS of order n.
Computational results on the spectrum of r-orthogonalities of sets of Latin Squares
For more information see:

