Ejercicios sobre algoritmos de grafos

Ejercicio 1:

Explica como corre el algoritmo de Shortest Paths de Dijkstra en el siguiente grafo, comenzando desde el nodo C.

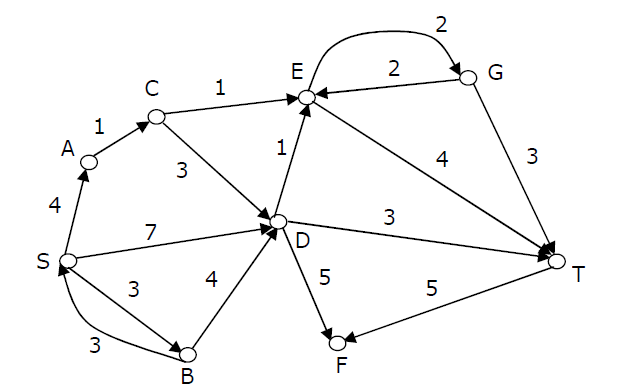
Ejercicio 2

Imagina que todos las artistas del grafo de arriba son no-dirigidas y los pares S y B, y E y G solo tienen una arista entre ellos (en vez de dos). Muestra cómo el algoritmo de Dijkstra escoge las aristas para formar un Minimum Spanning Tree.

Ejercicio 3

Considera la siguiente clase que implementa un grafo de vértices pesados (cada nodo tiene un peso). Implementa un member function llamado unsigned int sumWeights(unsigned src) que suma los pesos de los vertices que son alcanzables desde el nodo src.

#include <iostream>
#include <vector>
using namespace std;

class digraphWV {
private:
    // la lista de adyacencias (un vector de vectores de enteros)
    vector< vector<unsigned int > > adj;
    vector <unsigned  int> weight;

public:
    // constructor que recibe la cantidad de vertices del grafo
    digraphWV(unsigned int vertexQty) {
        adj.resize(vertexQty);
        weight.resize(vertexQty);
    }

    // establece el peso del node u
    void setWeight(unsigned int u, unsigned int w);

    // añade una arista del nodo u al v
    void addEdge(unsigned int u, unsigned int v);
};


void digraphWV::setWeight(unsigned int u, unsigned int w) {
    weight[u] = w;
}

void digraphWV::addEdge(unsigned int u, unsigned int v) {
    adj[u].push_back(v);
}

int main() {
    digraphWV G(5);
    G.setWeight(0,10);
    G.setWeight(1,2);
    G.setWeight(2,7);
    G.setWeight(3,5);
    G.setWeight(4,100);

    G.addEdge(0,2);
    G.addEdge(0,1);
    G.addEdge(2,3);
    G.addEdge(2,4);

    unsigned int totalW = G.sumWeights(0);
    std::cout << totalW << endl;
    return 0;
}

Ejercicio 4

Muestra como el algoritmo de Kruskal determina el Minimum Weight Spanning Tree del siguiente grafo: