“Permutations play an important role in digital communications as they are used in applications ranging from speech encryption to coding theory and cryptography.”
What are Permutation Polynomials?
A permutation of a set is a rearrangement of its elements. For example, an anagram of a word is a permutation; the word fluster is an anagram for the word restful, both words are composed of the same letters or elements but posses a different order. A polynomial over a finite field is called a permutation polynomial (PP) if the associated function is a permutation of the field. The study of PP began in the 1800’s with Hermite and Dickson and it was further developed in the following century by Carlitz and others. Determining if a polynomial permutes is fairly easy, however, finding conditions for arbitrary polynomials to permute the field is complicated and questions are still arising. Curiosity of the nature of these polynomials in conjunction with novel applications to areas such as Cryptography and Coding Theory has brought more attention to and has motivated the study of PP. Emphasis is given to finding and constructing families of PP that posses properties which are beneficial for applications.
One application that was discovered early on was the use of permutations of elements, the basis of a cipher alphabet, to construct cryptographic systems.
Example:
Consider the following message:
researchingpermutationpolynomialsrules
We encrypt this message using a PP over the field of seven elements. To do this, we first divide the message into seven letter blocks:
researc hingper mutatio npolyno mialsru les
Since the last block has only three letters, we add padding. In this example, we use the letter x as padding. Now our blocks are:
researc hingper mutatio npolyno mialsru lesxxxx
The PP we use is $f(x)=x^4+3x$ which generates the following permutation:
$$
f= \left(\begin{matrix}
0 & 1 & 2 & 3 & 4 & 5 & 6 \\
0 & 4 & 1 & 6 & 2 & 3 & 5
\end{matrix}\right)
$$
We apply this permutation to each block, for example, the first block would be:
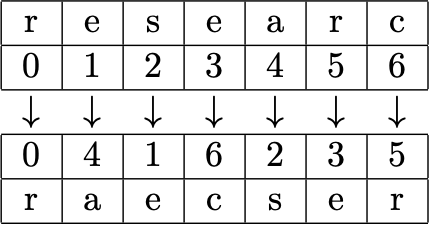
Applying this method to all of the blocks, we have:
researc hingper mutatio npolyno mialsru lesxxxx
raecser hpirnge mtuotai nypooln msiualr lxexsxx
Putting the blocks back together, the final cypher is:
raecserhpirngemtuotainypoolnmsiualrlxexsxx
An interesting exercise would be to decrypt this message applying the inverse of $f(x)$ in the same way as we did to encrypt.
