“Multidimensional arrays have many real-world applications in digital watermarking, multiple target recognition, and communications.”
What are a Periodic Arrays?
Many would agree that, in mathematics, the term “array” is quite vague. It does not have a well known, established, and precise definition as, say, a group. However, everyone has a good notion of what an array is: something that looks like a table or a matrix. One of the active areas of study in the Emmy Lab is the study of multidimensional arrays.
A one-dimensional array is something that can be described as a list, where the elements might be indexed using (a subset of) the natural numbers. Sequences are one-dimensional arrays. Two-dimensional arrays are list of lists; i.e., matrices. For indexing the elements in a two-dimensional array one requires pairs of natural integers, one number in the pair corresponding to the row; the other to the column. A three- dimensional array is a list of lists of lists; a list of matrices, where all the matrices have the same size. In general, an $m$-dimensional array is a list of lists of … of lists, where “list” appears $m$ times.
More precisely, one can define an $m$-dimensional array over the set $X$ as a function $A:\Lambda\to X$, where $\Lambda$ is a finite rectangular subset of $\mathbb{N}^m$. Using the usual notation $[n] = \{1, 2, \dots, n\}$, $\Lambda = [n_1]\times[n_2]\times\cdots\times[n_m]$ for some natural numbers $n_1, n_2, \dots, n_m$. Informally, we say that for $\alpha\in\Lambda$, $\alpha$ is a position of the array $A$, and $A(\alpha)$ is the value (from $X$) that the array holds in position $\alpha$. For a matrix $A$, we usually write $a_{i,j}$ for the element in the position $(i,j)$. If we see $A$ as an array, using our notation, $A(i,j) = a_{i,j}$. We are particularly interested in binary arrays; those for which $X = \{0,1\}$.
Instead of considering finite arrays, as defined above, one could consider \emph{infinite} arrays, where the index set $\Lambda = \mathbb{N}^m$; hence, the index set is no longer finite. A very special type of infinite arrays are \emph{periodic arrays}; those that are constructed by sticking together copies of the same finite array throughout the whole space. Multidimensional periodic arrays have many real world applications in digital watermarking, multiple target recognition, and communications, just to mention a few.
The Emmy Lab has active research in two main areas under the umbrella of periodic arrays: linear complexity and Costas arrays.
Linear Complexity
There is a well known definition of linear complexity of sequences, i.e., one-dimensional arrays, but that definition does not work for arrays of higher dimensions. For sequences, the linear complexity is the degree of the minimal polynomial that satisfies a linear recurrence relation on the entries of the sequence. Intuitively, the linear
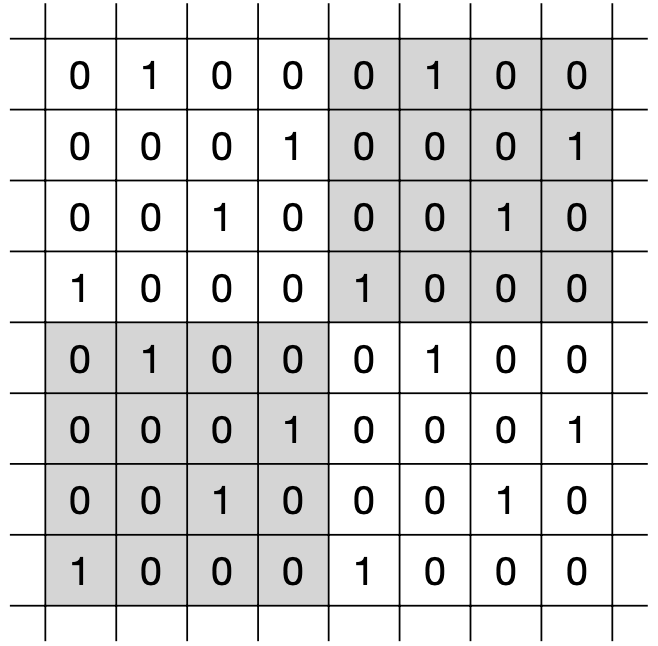
Figure 1: A (piece of) binary two-dimensional periodic array. Notice how the $4\times4$ pattern in gray is repeated.
complexity of a sequence is the least number of elements from the sequence that are needed to generate, using linear combinations, the whole (possibly infinite) sequence. The latter, more intuitive notion, can be formalized and generalized to higher dimensions. In the Emmy lab, we study the linear complexity of multidimensional periodic arrays, especially binary arrays that are constructed using the composition method.
Costas arrays
A Costas array is a two-dimensional permutation array, that is, a binary square matrix with exactly a single 1 in each row as well as a single 1 in each column, and the rest of the entries are zero; with the additional property that all the vectors joining pairs of 1’s are all distinct as vectors, i.e., differ either in their slope or their length. The latter property (distinct vectors) is known as the Costas property, and can be equivalently defined in different ways. Costas arrays where proposed by John P. Costas to enhance the performance of active sonars used in submarines. In the Emmy lab, we are interested in studying Costas arrays preserving the Costas property when extended periodically through the whole space. Moreover, we proposed a novel definition for higher-dimensional Costas arrays and we study the periodical extensibility of the Costas property in the multidimensional context.
